Can numbers tell us about the structure of the universe? Perhaps they can. Within the internal structure of integers is embedded information that may shed some light. In what follows I will share some interesting if generally overlooked features of numbers and basic arithmetic.
In 1202 AD, Fibonacci said:
“These are the nine figures of the Indians: 9 8 7 6 5 4 3 2 1. With these nine figures, and with this sign 0 which in Arabic is called zephirum, any number can be written, as will be demonstrated.”
One of the first lessons children are taught about mathematics is that all numbers exist on a construct called the number line.
The number line readily supports learning about how numbers can be used to add and subtract numbers by traversing distances to the right and left along the line. If one wants to involve higher dimensions through multiplication, exponents, division and square roots, then one can turn 90 degrees for each new dimension, extend the number line into that dimension and begin measuring the areas and volumes contained by these spaces.
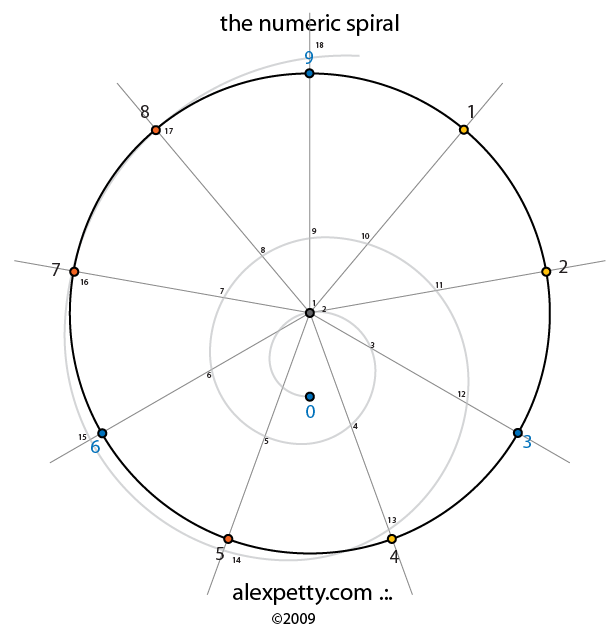
All of this geometry works out fine when dealing with life within the normal range of experience, however, are layers of important meaning lost by not taking into account the underlying information which the numbers themselves indicate about how they are actually positioned in relation to one another? Is there a way to place numbers upon a spiral whose form is governed by the Golden Ratio?
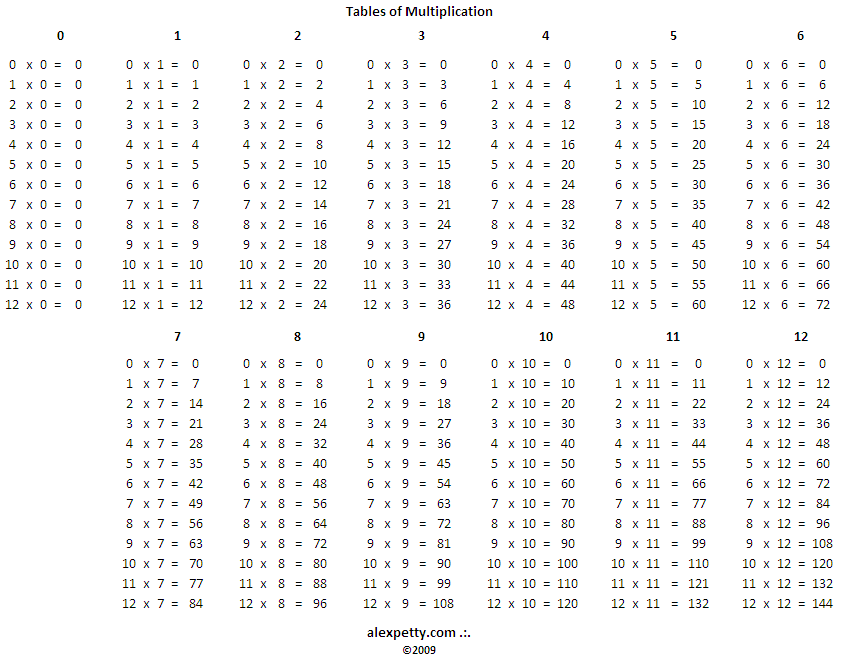
Let’s look more carefully at what it means to multiply numbers together. Here are the multiplication tables taught to grade school children.
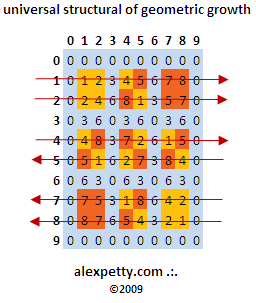
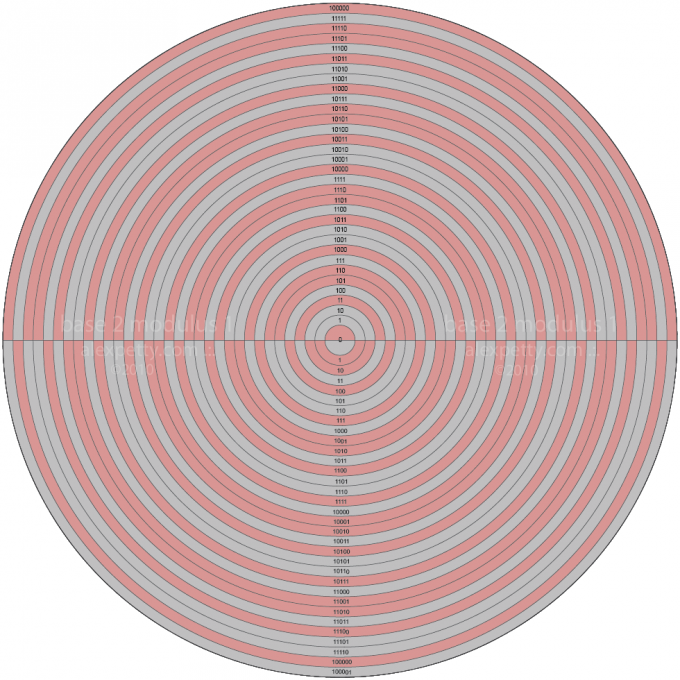
Although the above table is a clear expression of the geometric growth of numbers in two dimensions, it perhaps does not offer the complete picture. When numbers are instead considered as points on a spiral that is intersected by 9 radial divisions (i.e., using 9 digit clock-math or modulus 9), one can then represent the tables of multiplication this way:
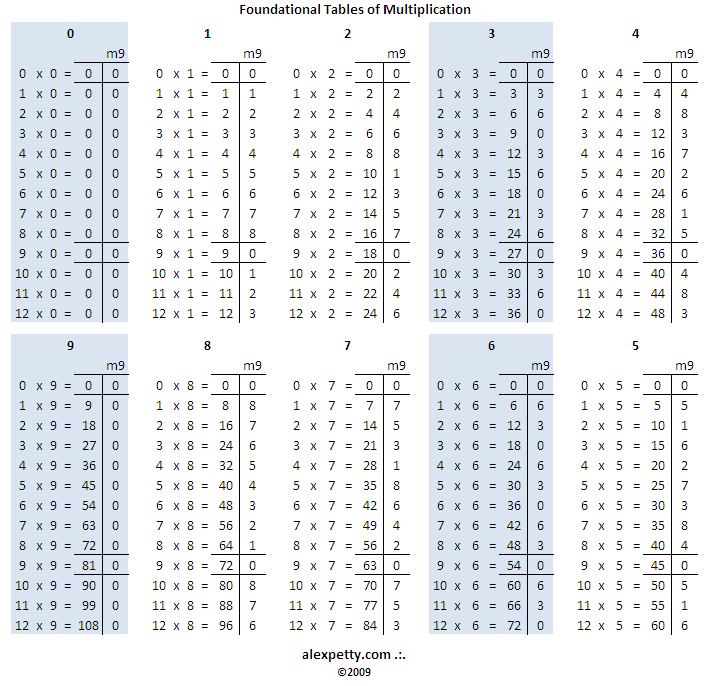
We can derive the following structure from the table above:

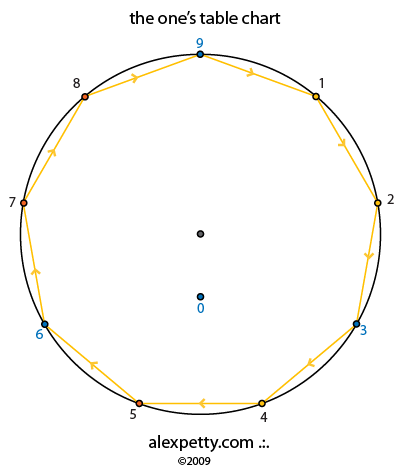
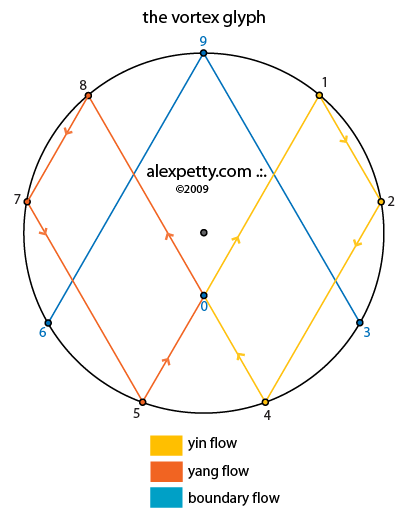
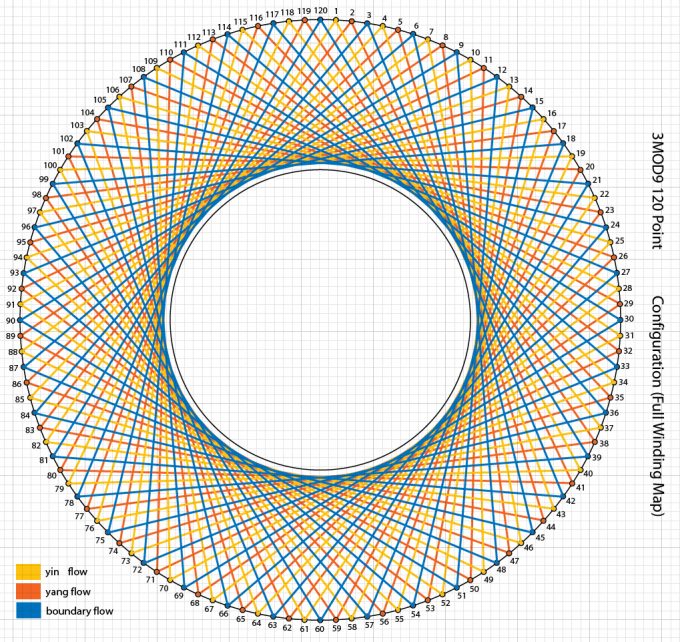
Each multiplication table for numbers 1 through 9 possess what I call a unique “flow signature”.
The flow signature for the one’s table is given below.
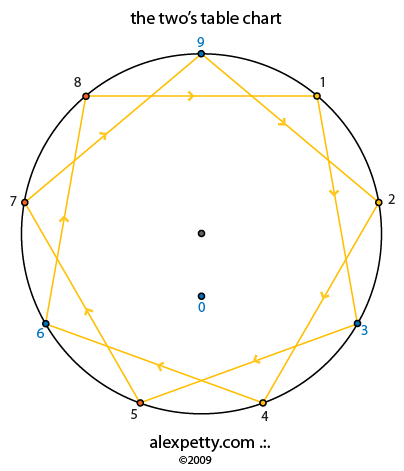
The flow signature for the two’s table is given below.
The flow signature for the three’s table is given below.
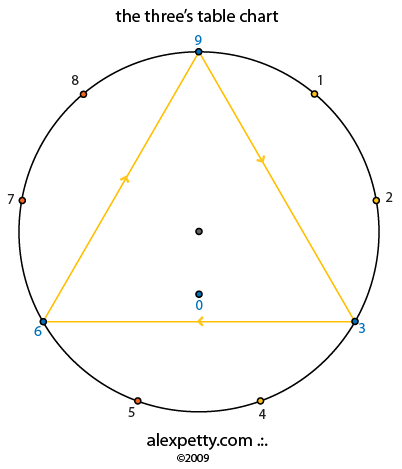
The path of three traces the enclosed equilateral triangle 3 times.
The flow signature for the four’s table is given below
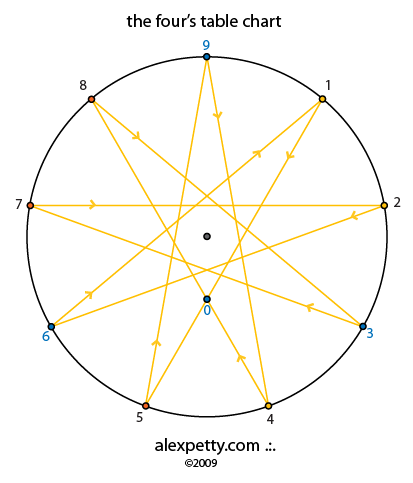
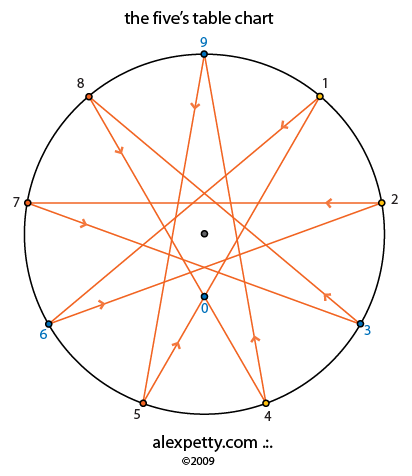
The flow signature for the five’s table is given below. Note that between 4 and 5 lies the path through the singularity; the zero point. Once crossed the direction of the flow is reversed.
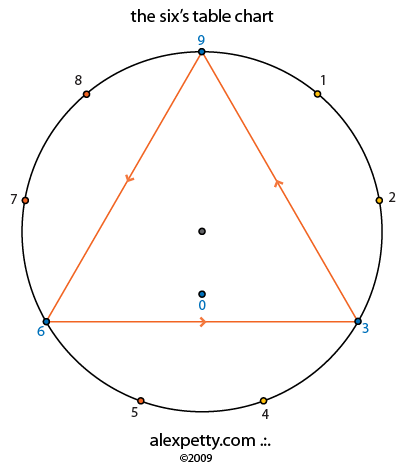
The flow signature for the six’s table is given below.
Here again, the enclosed triangle is lapped three times, though, in the opposite direction of the three’s table.
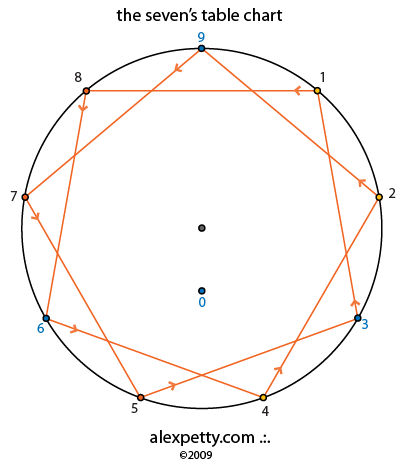
The flow signature for the seven’s table is given below.
The flow signature for the eight’s table is given below.
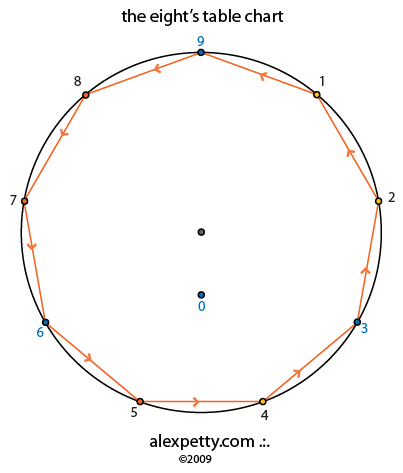
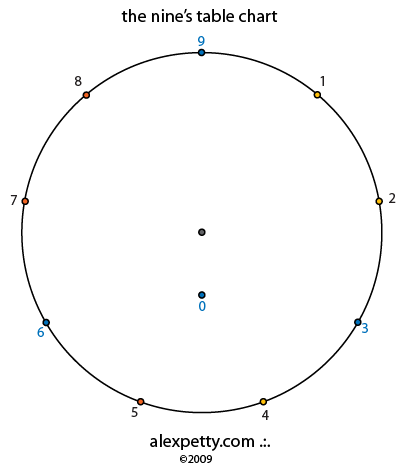
The path of nine has no component and is therefore always zero. It is a perfect unperturbed circle.
Once again, the shapes formed in the charts above are derived from the universal structure of geometric growth.
The sequences that arise from the foundational multiplication tables can be summarized as follows:
By organizing the numbers 1 through 9 and by observing how these relate to each other, we can begin to discern the
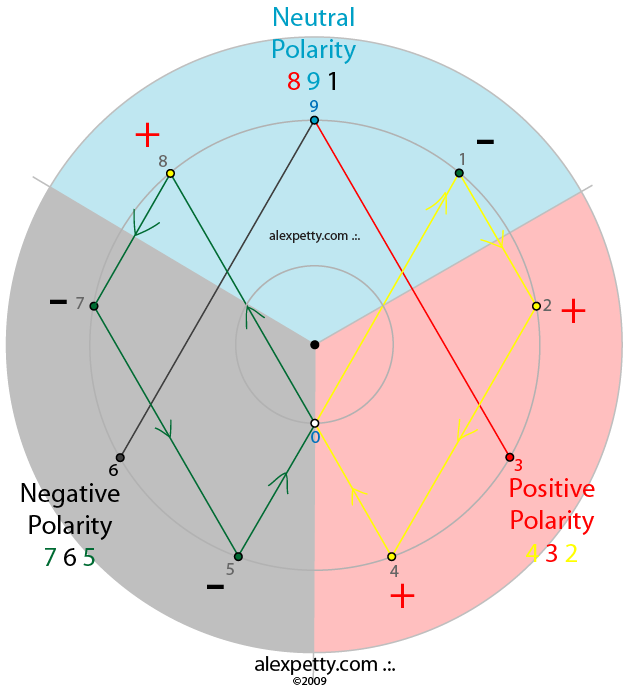
We also can begin to see how polarized forces shepherd form through physical expansion (doubling) and contraction (halving).
In doubling (expansion):
1 becomes 2
2 becomes 4
4 becomes 8
8 becomes 16 (mod 9) = 7
32 becomes 64 (mod 9) = 5
64 becomes 128 (mod 9) = 1
and so on.
In halving (contraction):
1 becomes 0.5 (mod 9) = 5 1
0.5 becomes 0.25 (mod 9) = 7
0.25 becomes 0.125 (mod 9) = 8
0.125 becomes 0.625 (mod 9) = 4
0.625 becomes 0.03125 (mod 9) = 2
0.03125 becomes 0.015625 (mod 9) = 1
and so on.
Here we have all the infrastructure needed to account for the expansion and contraction of physical systems within Creation.
.:.
1. The way to compute clock math for numbers less than 1 is to add the decimal digits together. For example 0.625 would be handled as “0+6+2+5=13, 1+3=4”. For repeating decimals, continue the process until a 9, or 0, is reached. For example, 0.|6| (meaning 6 repeating) would be handled as “6+6+6=0, since 6+6=12, 1+2=3 and then 3+6=9=0”. This procedure also works for numbers larger than 1.

Mr. Petty, with utter amazement at what I have found here on your site, it would seem that you and Pythagoras have more than numbers in common. Although I have been remiss in my mathematics research, I have come full circle with exposure to a mathematical theory that places ALL of these exact correlations into the hydrogen atom, at the beginning of the universe.
I am working with a math genius who has discovered the math patterns that create the hydrogen atom, and the Cosmic Microwave Background. It would seem that there is so much more involved here with an utterly precise mathematical pattern that cannot possibly be randomly formed or assembled by chance. It is the wedding of the numbers and frequencies that says it all.
Stay tuned for publication in April