It occurs to me that the number of points needed for a coordinate system to allow the definition of form across a desired number of dimensions is given by “two to the power of d” where d is the number of dimensions you are interested in working with. See the table below.
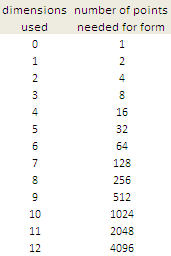
To me, this table suggests that the universe increases its expansion into dimensionality by using the expanding and contracting paths of doubling and halving itself into whatever configuration the creative or destructive will requires for manifestation.
It also suggests that in a system operating without dimension,
To define form in one dimension, it is necessary to define a coordinate system that uses two points as predicted by 2^1 = 2.
To define form in two dimensions, a coordinate system using four points is needed as predicted by 2^2 = 4.
To define form in three dimensions, a coordinate system using eight points is needed as predicted by 2^3 = 8.
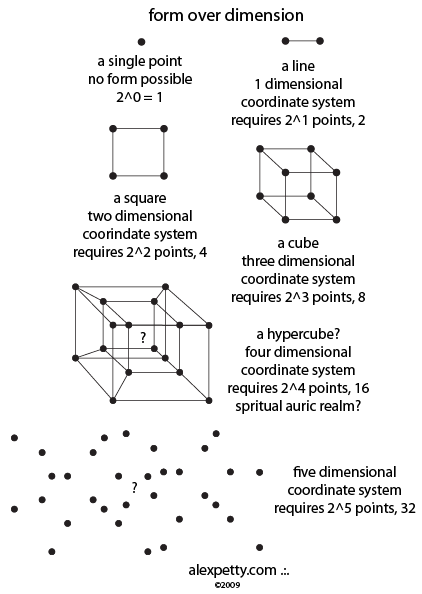
It stands to reason that form in four dimensions requires a coordinate system using 16 points (as predicted by 2^4 = 16), as arranged as shown above. I believe a 5th physical dimension would require a 32 point based coordinate system to describe a 5-dimensional form and so on. It also stands to reason that a “hypercube” may require a 4th, 5th and 6th dimension – one parallel dimension to each of the 3 dimensions that we normally experience.
The Zero Dimension Case
“a to the power of zero equals 1″
Anytime the you have “a/a”, it equals one.
Algebraically stated “a/a=1″ can be written “a to the power of 1
Said plainly, when you have all the pieces of a pie then you have one whole pie. So then 1/1=1, 2/2=1, 5/5 = 1, 10/10 = 1, 100/100=1 and so on. In a zero dimensional universe, the pie is the universe. It is the universal Mind in stillness, unfettered by the restless force of creative or destructive will and thus in a state of perfect self-unity.
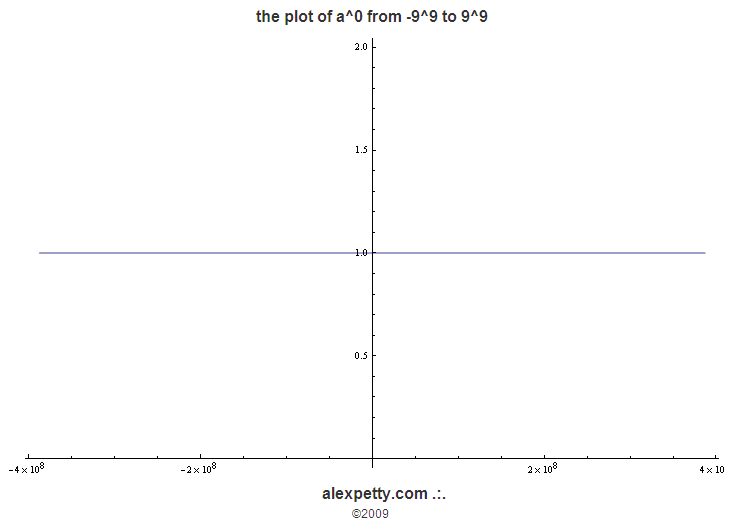
Looking at this from the two-dimensional perspective, take a^0 (a to the zero power) and let the value of “a” approach some large value (say 9^9). You will see that it remains forever 1. In other words, when you let “a” dwell on zero, even when you greatly increase its “size”, the universe will always respond, “Here at zero, all is one: there are no dimensions, there is no distance, there is no time needed for traversing space, etc. There is only unity. There is only oneness. All is one.”
Let’s look at this another way. When you evaluate sequential numbers raised to the “power of zero” and then reduce these to mod9 values, the result is the following table.
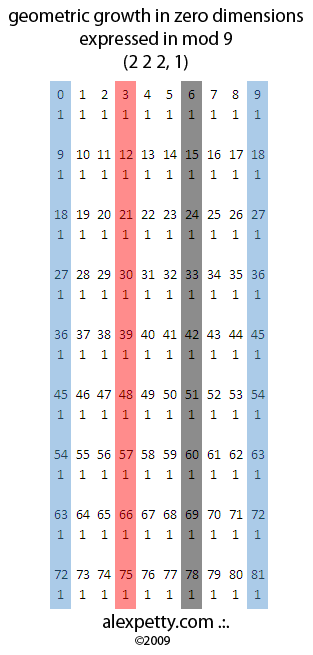
I interpret the table above by looking for two parameters which I call:
1) Growth Signature (GS)
2) Increment Line Sum (ILS)
The Growth Signature (GS) is made up of three numbers which are each MOD9 expressions of the sum of the digits found in columns 1 & 2, 4 & 5 and 7 & 8. Taking the above table as an example, this would be obtained by adding 1+1 from the 1 & 2 columns, 1+1 from the 4 & 5 columns and 1+1 from the 7 & 8 columns giving a GS = 2 2 2. I have found that for all dimensions 2 and higher, GS = ILS in mod9.
The ILS is the sum of all the digits in a given incrementation of 9 stated in MOD9. In this particular case ILS = 1 because 1+1+1+1+1+1+1+1+1+1 = 10 = 1.
The key parameters for this table are 2 2 2, 1. In this
One Dimensional Growth
The standard view of 1 dimensional growth is seen below.
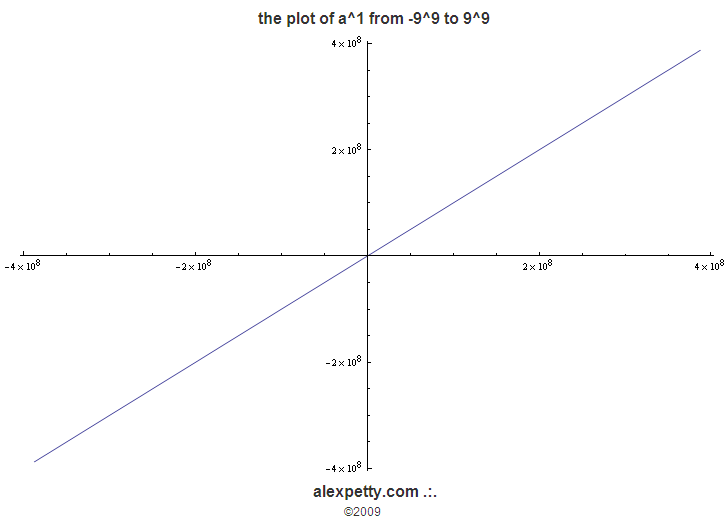
When one evaluates the infinite sequence of numbers raised to the “power of one” and reduces these to mod9 values, the following table is the result.
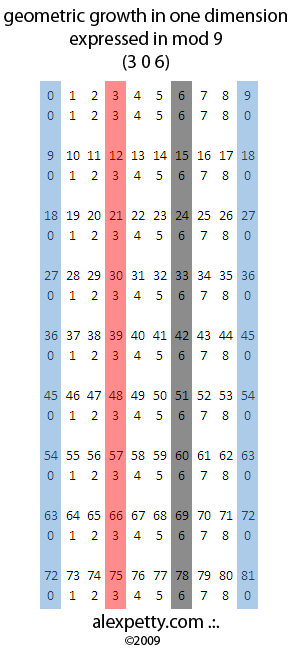
The universe is very linear as it grows over one dimension. Here the pole at 3 is always equal to 3 and the pole at 6 is always equal to 6. We also see that the pole at 9 is no longer a “physical” part of the system as its value is always zero. In this table GS=3 0 6 and ILS = 0.
Note that in mod9, the ten number sequence we use to calculate the ILS never changes in any increment. The numbers reoccur in every incrementation of nine in exactly the same way for as high as you care to go. The highest incrementation of 9 that I verified was of the order 9 x10^31,000.
Two Dimensional Growth
The standard view of 2 dimensional growth is seen below.
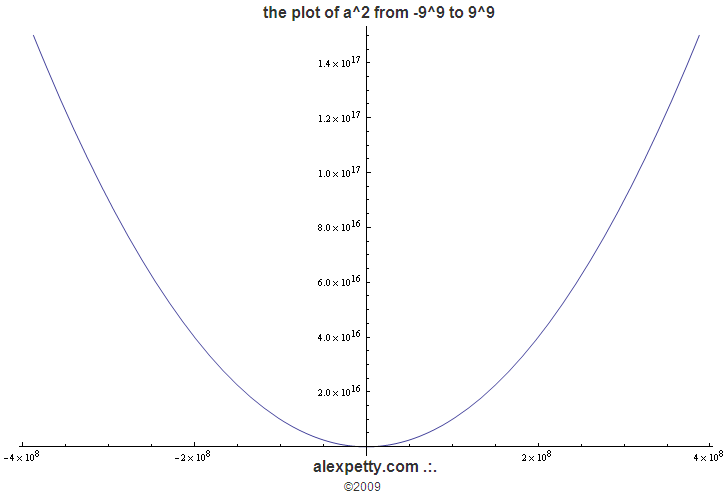
When one evaluates the infinite sequence of numbers raised to the “power of two” and reduces these to mod9 values, the following table results.
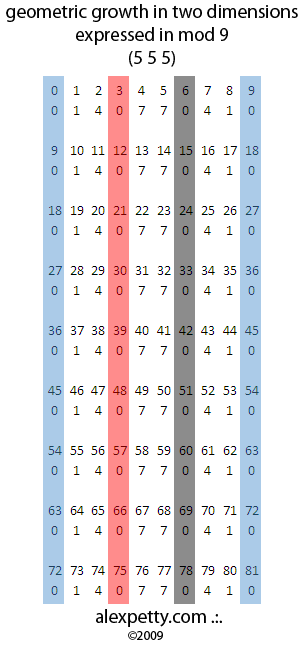
From the second dimension through all higher dimensions, we see that the poles at 3 and 6 as well as 9 will always be equal to zero. We also begin to observe interesting resonances in the channels of contractions and expansion at 124 and 875. Note that “square geometric growth” produces a palindromic sequence of 1 4 7 7 4 1. Note also that the ILS is 24 (or 6) and the GS is 5 5 5 (also 6).
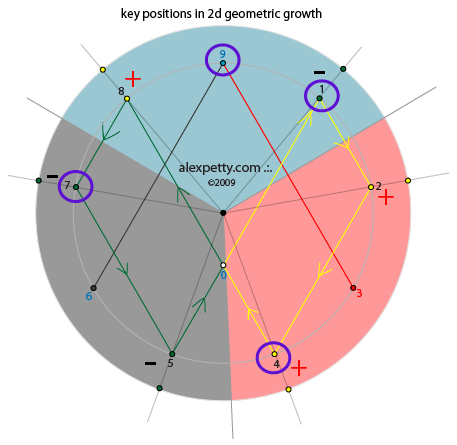
Three Dimensional Growth
The standard view of 3 dimensional growth is seen below.
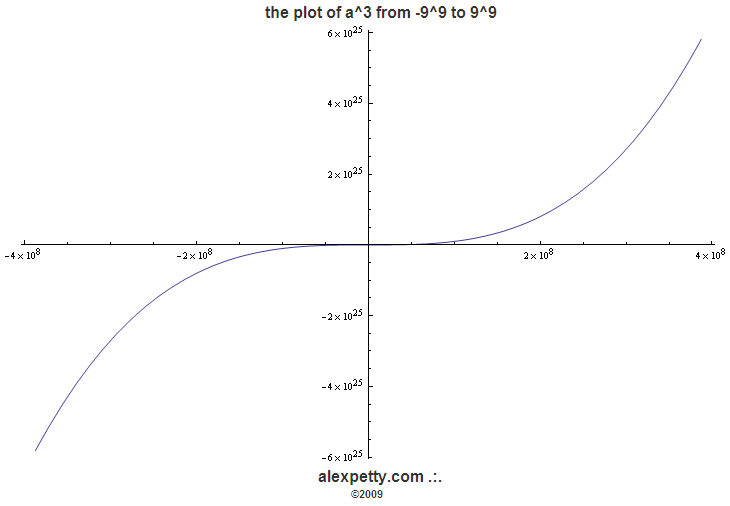
When one evaluates the infinite sequence of numbers raised to the “power of three” and reduces these to mod9 values, the following table results.
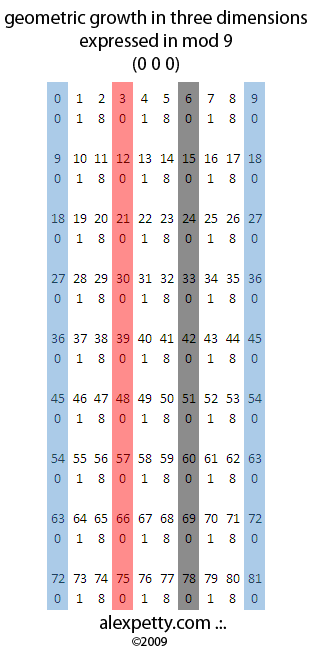
Note that the ILS is 0 and the GS is 0 0 0.
I have developed a chart showing the Growth Signatures for 36 dimensions. It is very interesting to see that a pattern arises.
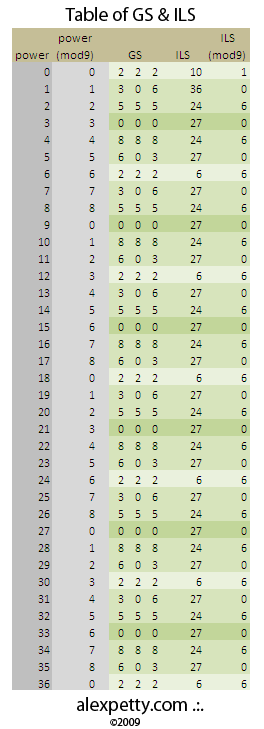
The Growth Signature pattern is wave-like, with a peak at 0 0 0 and a trough at 2 2 2. It cycles endlessly:
0 0 0 –> 8 8 8 –> 6 0 3 –> 2 2 2 <– 3 0 6 <– 5 5 5 <– 0 0 0
Also, the ILS pattern alternates infinitely between 0 and 6 (Universal Mind and the Negative Pole respectively).

I would ask you to consider my proposals for DIMENSIONS and a dimensional progression for universal formation – https://godtheory.empiricalchurch.org/Moshehs-Unifying-Field-Theory/ — you might really like this… or hate it.